世の中には2種類の人間がいる... という文句、妙に説得力がありそうで、この後主語もスケールも大きい名言が続きそうなやつ。
人間だけではなく疑似乱数についても、2種類に分けられるらしい。

「世の中には2種類の疑似乱数がある、次の出力を予測できるか出来ないかのどちらかだ」 ¹

あるサイトに登録したときメールで、https://example.com/register/?token=blquu5jrdrmd のようなユーザー認証用のリンクが送られてくることがある。通常、token にはその人以外が知りえない（総当りしようとすると数年〜数千年位じゃ終わらない）ようなランダムな文字が渡されている。なのでこのリンクをクリックして開いた人は、そのメールアドレスの所持者であるということを証明できる。もし、この token が簡単に予測できるとしたら、この「ユーザー認証」自体が成り立たなくなる。²

この token はおそらく自動で生成しているが、これはコンピューターが計算で求めた「疑似乱数」を元にしている。その疑似乱数には「暗号論的擬似乱数生成器」と呼ばれる、出力される乱数の予測が困難なものと、そうでないものがある。

例えば Python の random モジュールは予測可能な乱数であるので、もしこれを使って例の token を作ってしまうと認証が安全なものとは言えなくなってしまう。

メルセンヌツイスタは完全に決定論的であるため、全ての目的に合致しているわけではなく、暗号化の目的には全く向いていません。
random --- 擬似乱数を生成する — Python 3.12.0 ドキュメント

import random
r = random.random()

また、JavaScript では Math.random を利用できる。これはランタイムによって実装が異なるとは思うが、Node.js や Chrome で採用されている V8 では、xorshift128+ が使われているよう。Firefox や Safari も同じアルゴリズムになっているっぽい。そして、こちらもメルセンヌ・ツイスタ同様に、予測可能（暗号学的に安全ではない）乱数なので予想できてしまうとまずい用途には利用しちゃいけない。

we decided to reimplement Math.random based on an algorithm called xorshift128+
（中略）..even though xorshift128+ is a huge improvement over MWC1616, it still is not cryptographically secure.
There’s Math.random(), and then there’s Math.random() · V8

const r = Math.random()

Python では secrets というモジュールを利用することで、暗号学的に安全な乱数が作成できるので、こちらを使う必要がある。言語によって色々な「暗号学的に安全な乱数」を生成できるモジュールが準備されているはずなので、用途に応じて使い分ける。³

secrets モジュールを使って、パスワードやアカウント認証、セキュリティトークンなどの機密を扱うのに適した、暗号学的に強い乱数を生成することができます。
secrets --- 機密を扱うために安全な乱数を生成する — Python 3.12.0 ドキュメント

import secrets
r = secrets.token_hex(8)

python の secrets モジュールの実装を追ってみると、os.urandom() を元に乱数を作成していた。Linux 環境では getrandom() というシステムコールが呼び出されるそう。
getrandom() は /dev/random という疑似デバイスから乱数を取得する。これはデバイスドライバー等の入出力から得られた情報を環境ノイズとして集めて、「真の乱数」として使えるようにすることを目的にしているものらしい。

/dev/random - Wikipedia

環境ノイズを元に乱数を生成するものの他に、暗号学的に安全な乱数の生成の方法として暗号学的ハッシュ関数に通すやりかたもあるらしい。

暗号学的に安全ではない乱数は、本当に予測できるのか？

メルセンヌ・ツイスタや xorshift は予想できて、環境ノイズから作られた乱数は予想できないというのは本当なのか？
暗号学的に弱い乱数が予測できると言われているのは、出力には周期性があるためで何度か乱数を出力しているといずれ、昔出てきた乱数のパターンが現れるからであるそう。

例えば、先程見た乱数生成アルゴリズムの周期は以下のようになっている。

メルセンヌ・ツイスタ --> 2¹⁹⁹³⁷ - 1
xorshift128+ --> 2¹²⁸ - 1

xorshift128+ では例えば最初に「192 → 41 → 12」の順で出力された後、2¹²⁸ - 1 回後にはまた「192 → 41 → 12」が出てくるという意味。

ちょっと128bit だと時間的に大変そうなので、32bit バージョンの xorshift で試してみた。
周期は 2³² - 1なので、関数の返り値が 2³² - 1 回後も全く同じになるのかを見てみる。

※ 実装は Xorshift - Wikipedia からほぼコピペ

#include <stdio.h>

unsigned int xor32(void) {
  static unsigned int y = 2463534242;
  y = y ^ (y << 13);
  y = y ^ (y >> 17);
  y = y ^ (y << 5);
  return y;
}

int main(void){
    unsigned int r1 = xor32();
    printf("r1 is %u\n", r1);  // 723471715

    for(long i=0; i<4294967295 - 1; i++){
        xor32();
    }

    unsigned int r2 = xor32();
    printf("r2 is %u\n", r2);  // 723471715
}

2³² - 1 回後に全く同じ数字が出てきた！当然なのだろうけどおもしろい！！

つまり、もし最初の例の token を生成するのに使用した乱数に周期性がある場合、何度か token を作らせてみてその並び順から現在の乱数の状態を予測できる。その状態と利用しているアルゴリズムがわかれば、そこから次に出力される乱数がバレてしまう。

以降は2種類の疑似乱数生成器の出力を眺めてみる。

暗号論的擬似乱数生成器

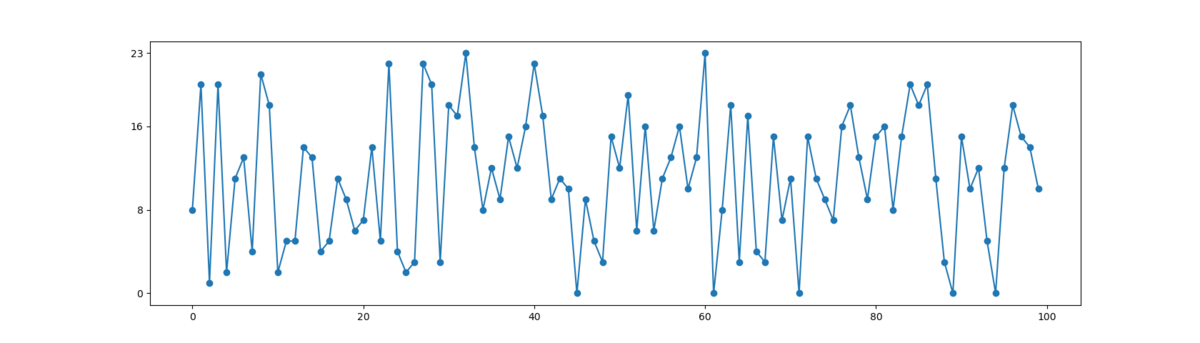
先ほど紹介した、Python の secret モジュールを使い、0~23 の乱数を100個生成してみた。
数列を眺めても良くわからないのでグラフで見てみる。これだけで完全にランダムだと言い切るのは無理はあるけれど、なんとなく出力に偏りはなさそうに見える。（ランダム性の証明ってできるのか？）

import secrets
from matplotlib import pyplot as plt

fig = plt.figure()

r = []
for i in range(100):
    r.append(secrets.randbelow(24))
    print(r[-1], end=", ")
    
plt.yticks([0, 8, 16, 23])
plt.plot(r, "o-")
plt.show()

8, 20, 1, 20, 2, 11, 13, 4, 21, 18, 2, 5, 5, 14, 13, 4, 5, 11, 9, 6, 7, 14, 5, 22, 4, 2, 3, 22, 20, 3, 18, 17, 23, 14, 8, 12, 9, 15, 12, 16, 22, 17, 9, 11, 10, 0, 9, 5, 3, 15, 12, 19, 6, 16, 6, 11, 13, 16, 10, 13, 23, 0, 8, 18, 3, 17, 4, 3, 15, 7, 11, 0, 15, 11, 9, 7, 16, 18, 13, 9, 15, 16, 8, 15, 20, 18, 20, 11, 3, 0, 15, 10, 12, 5, 0, 12, 18, 15, 14, 10,

暗号論的擬似乱数生成器で作成した乱数列

周期が極端に短い疑似乱数生成器

ついでに、線形合同法という疑似乱数生成アルゴリズムを使い周期がかなり短い乱数を作ってみて、どのように出力が出てくるのかを眺めてみる。線形合同法というアルゴリズムを使い、周期が24というかなり短い周期の疑似乱数生成器を用意する（線形合同法 - Wikipedia から写しただけ）。

#include <stdio.h>

unsigned int lcg(){
    static unsigned int x = 8;
    unsigned int a = 13;
    unsigned int b = 5;
    unsigned int m = 24;
    x = (a * x + b) % m;
    return x;
}

int main(void){
    for(int i=0; i<100; i++){
        printf("%u, ", lcg());
    }
}

13, 6, 11, 4, 9, 2, 7, 0, 5, 22, 3, 20, 1, 18, 23, 16, 21, 14, 19, 12, 17, 10, 15, 8, 13, 6, 11, 4, 9, 2, 7, 0, 5, 22, 3, 20, 1, 18, 23, 16, 21, 14, 19, 12, 17, 10, 15, 8, 13, 6, 11, 4, 9, 2, 7, 0, 5, 22, 3, 20, 1, 18, 23, 16, 21, 14, 19, 12, 17, 10, 15, 8, 13, 6, 11, 4, 9, 2, 7, 0, 5, 22, 3, 20, 1, 18, 23, 16, 21, 14, 19, 12, 17, 10, 15, 8, 13, 6, 11, 4,

周期が極端に短い疑似乱数生成器による乱数列

こんなの乱数っていえるかよ！（疑似乱数なので当然だけど）

暗号学的な強度が求められているときはもちろん、十分無作為である必要があるときに自作の乱数を使ってしまうと大変なことになりそう。

予測してないじゃん！と思ったあなたへ

実際に予測する記事書きました

burion.net

電動ダイスカップサイコロ振り機自動ダイスカップゲームイベントパーティーダイス5個付属

ノンブランド品

Amazon

ウォール街のランダム・ウォーカー＜原著第13版＞株式投資の不滅の真理

作者:バートン・マルキール
日経BP

Amazon

さっき牛丼を食べながら思いつきました↩
自動生成のイメージしやすい例として URL に付与される token を上げた。しかし、実際はこのケースの総当たり（オンライン攻撃）は通信が必要になるため試行速度はレイテンシで制限されてしまう。それは本質的ではなく、ここで考えたい「予測の難しさ」は ZIP ファイルのパスワードの総当たりの様に（オフライン攻撃）最先端の非常に強力なコンピューターを使って高速に試行したとしても成立するレベルの難しさを意図している。↩
逆に暗号的な強度は不要で乱数生成速度を重視したい場合は「暗号的に安全な乱数」は向かない。アルゴリズムによると思うが getrandom() では乱数生成に必要なエントロピーが溜まるまでは処理をブロックするため遅くなるし、暗号学的ハッシュ関数を通す場合も必要な処理が増えるためパフォーマンスは出しにくい思う。↩